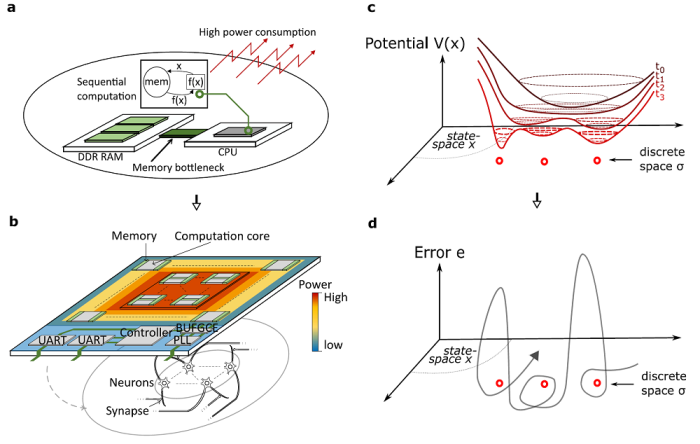
Among the theories needed to bridge machine and human intelligence, the Ising model has proven useful for capturing mesoscopic neuronal interactions by simplifying their activity to binary decisions. In this model, neural states representing stable memories may be organized into an “energy” landscape with local and global minima. The transient neural dynamics required to reach these states are classically understood as gradient descents, like a ball going downhill (see Fig. 1c). However, insights from the statistical physics of spin glasses, awarded the Nobel prize in Physics this past year, predict that the energy landscape is "rough” with many local minima that tend to prevent gradient descent dynamics to efficiently achieve transitions to lower energy states. These local minima place limitations on the computational power of Ising models, since finding lower energy states is equivalent to hard combinatorial optimization problems that even supercomputers cannot easily solve rapidly (Fig. 1a).
In groundbreaking work published in the journal Communications Physics, Project Associate Professor Timothee Leleu and Professor Kazuyuki Aihara at The University of Tokyo International Research Center for Neurointelligence(WPI-IRCN), in collaboration with collaborators at Institute of Industrial Science, The University of Tokyo, the University of Bordeaux (France), and the Massachusetts Institute of Technology (USA) demonstrate that lower energy states can be reached much faster with non-relaxational dynamics involving the destabilization of nontrivial attractors in a recurrent neural network. The key to this approach is a scheme called chaotic amplitude control that operates through the heuristic modulation of target “amplitudes” of activity (see Fig. 1d). Importantly, this method exhibits improved scaling of time to reach global minima, suggesting that such neural networks could, in principle, solve difficult combinatorial optimization problems. Conventional computers cannot easily solve these problems, so the authors developed a neuromorphic computing system (see Fig. 1b) using a field programmable array to solve problems with improved scaling.
The instantiation of non-relaxational dynamics may facilitate the development of new Ising machines with greater speed and efficiency in problem solving. In complex biological systems like the human brain, chaotic amplitude control might help to facilitate cognition in tasks that are combinatorial such as image segmentation or complex decision making. Project Associate Professor Leleu and the team will pursue further solutions and enhancements in high performance combinatorial optimization via a collaboration between the IRCN and NTT Research.
Reference: Leleu, T., Khoyratee, F., Levi, T., Hamerly, R., Kohno, T. and Aihara, K., Scaling advantage of chaotic amplitude control for high-performance combinatorial optimization. Communications Physics, 4(1), pp.1-10, 2021
The link to the article is as follows: .https://www.nature.com/articles/s42005-021-00768-0
Media Contact: The authors are available for interviews in English.